球面光學成像系統:單折射面成像和球面反射鏡成像
1、單折射面成像
對B點的物點而言,BB'相當于其光軸(輔軸),那么B一定成像于B'點。AB上每一點都如此,那么,A'B'就是AB的完善像。

㈠ 垂軸放大率β
定義β=y'/y
∵ ΔABC相似于ΔA'B'C'
∴-y'/y=(l'-r)/r-l
利用n'(1/r-1/l')=n(1/r-1/l)
若n=n'無界面
→ l=l' β=1未成像,無意義
(l'-r)/r-l=-n/n' l'/l=-y'/y
注意:垂軸放大率是物截距l的函數,即物點位于不同位置其β是不同的。
∵ n'/l'-n/l=(n'-n)/r
l'/n'=1/[(n'-n)/r+n/l]
∴ β=n/l*l'/n'=n/l/[(n'-n)/r+n/l]
=1/[1+(n'-n)/r*l/n]∝1/l或l
n'>n時,β∝1/l
n'<n時,β∝1/l
討論
補充一點:一個沿軸向有一定厚度的物經成像后,其軸向高度將不再與物相似。如圖所示:

(二)軸向放大率α
當物沿光軸有一微小位移dl時,引起像亦有一微小位移dl'討論>
①
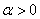 ,物像點向相同方向移動
,物像點向相同方向移動
②
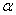 也與物點位置有關,不同點有不同的軸向放大率,亦即像要變形。
也與物點位置有關,不同點有不同的軸向放大率,亦即像要變形。
(三)角放大率
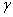
定義:一對共軛光線與光軸的角之比
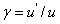 為角放大率。
為角放大率。
利用
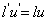
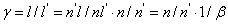
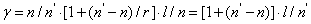
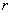 小,
小,
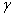 越大 (當
越大 (當
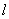 一定時)
一定時)
不難看出三者之間關系:
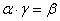
又
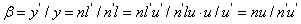
∴
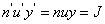 (拉格朗日-赫姆霍茲不變量)
(拉格朗日-赫姆霍茲不變量)
簡稱拉赫不變量,它表征了光學系統的性能。
迄今為止,我們已經知道三個不變量:
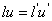
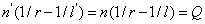 阿貝不變量
阿貝不變量
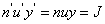 赫不變量
赫不變量
二、 球面反射鏡成像
凹鏡成像與凸鏡成像
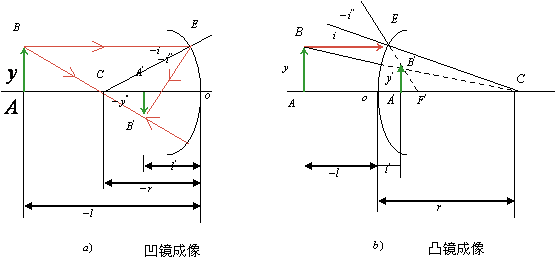
球面反射系統中,只要將球面折射系統中所得公式中的 代替,就可得到相
應即 通過球心的光線將沿光路返回,重匯于球心。
三、共軸球面系統
前面分析的是單個折射球面(反射)的成像特征及相應的光路計算.它們是構成光學系統的
小單元,對于由多個折、反球面構成的共軸光學系統而言只要找到相鄰兩球面間的光路關
系,剩下的問題就是逐個成像,逐個計算直至求出像。
㈠ 過渡公式將上述第二式與第四式對應項相乘,利用
得由拉赫不變量
(二) 成像放大率